About

Hello! I'm a physics PhD student at Caltech, pursuing research in theoretical high energy physics. Previously, I completed a bachelor's degree in Mathematics and Physics at the University of Toronto, as well as a Master's degree in theoretical physics at the Perimeter Institute.

I am deeply passionate about high energy theory, astrophysics, and computational physics, and have pursued research in each of these subjects throughout my undergraduate degree. At the Perimeter Institute, I explored aspects of quantum field theory and string theory, relativity and cosmology, and quantum gravity. If you'd like to learn more about my work, please visit my research page, or check out this theoretical high energy physics seminar that I delivered at the University of Toronto.

I was born and raised in downtown Toronto, until I moved out to the suburbs in the nearby town of Newmarket at the age of twelve. I later moved back to the city to attend university, where my childhood interest in physics ignited into a true passion. Aside from physics, I also have strong interests in history and computer science, which keep me occupied in my free time.

Research

Confinement on $\mathbb{R}^3 \times \mathbb{S}^1$ and Double-String Collapse

Supervised by Prof. Erich Poppitz

Confinement is a problem of great importance in quantum field theory, being the mechanism by which quarks are held together in hadrons. However, the mathematics of this mechanism in non-supersymmetric quantum field theories formulated on 4-dimensional spacetime $\mathbb{R}^{1,3}$ is intractable with current techniques. It is of interest, therefore, to study confinement in the environment of supersymmetric $SU(N)$ Yang-Mills theory (SYM) on $\mathbb{R}^{1,2} \times \mathbb{S}^1$, where one spatial dimension is compactified to a small circle $\mathbb{S}^1$. Here, confinement can be studied in a semi-classical, calculable environment.

Figure 1: Static quark sources confined by a "double string" consisting of two gluon flux tubes, which are domain walls interpolating between the $N$ vacua of $SU(N)$. Pictured is an $\mathbb{R}^2$ slice of the potential energy density of the bosonic fields, which are taken independent of the $\mathbb{S}^1$ coordinate. The gauge group is $SU(3)$.

Bub, Poppitz, & Wong (2021) performed a numerical study of confinement in this theory. Here, static quark sources are in general confined by "double strings" consisting of two BPS domain walls. This confinement mechanism holds for quarks of all $N$-alities, except for fundamental quarks (with $N$-ality $k = 1$), for which the domain walls collapse to form a single flux tube. I discussed this study in detail during this virtual seminar at the University of Toronto.

Compact-Object Mergers in the Galactic Centre

Supervised by Prof. Cristobal Petrovich

In Bub & Petrovich (2020) we investigated whether dynamical processes in the Galactic centre might enhance the rate of binary mergers, with particular emphasis on compact-object mergers of the type detected by the LIGO/Virgo gravitational wave detectors.

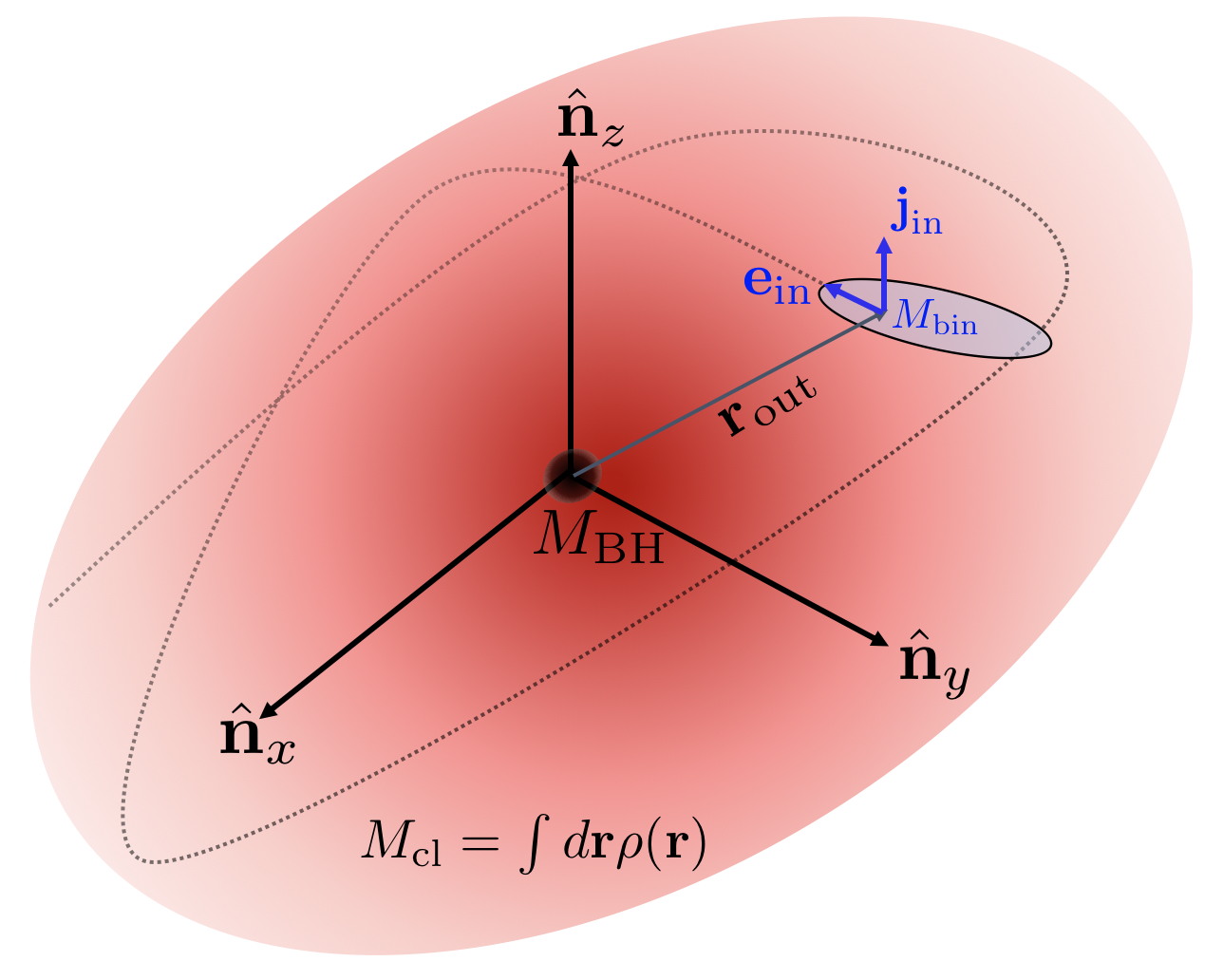Figure 2: A binary star system embedded within a triaxial nuclear star cluster containing a central supermassive black hole.

In this work, we determined that the combination of a central supermassive black hole (SMBH) and surrounding triaxial nuclear star cluster can greatly enhance the binary merger rate up to several parsecs from the Galactic centre. These mergers occur due to several distinct dynamical effects, including enhanced eccentricity modulations in binary systems which are similar to octupole-level modulations to the Lidov-Kozai effect in triple systems (Naoz 2016), as well as chaotic diffusion of eccentricities arising from overlapping dynamical timescales (Petrovich & Antonini 2017).

Resonance and Phase Mixing in the Galactic Disk

Supervised by Prof. Jo Bovy and Dr. Jason A. S. Hunt

Hunt, Bub, Bovy et al. (2019) examined how various models of the Galaxy's bar and spiral arms induce signatures of resonance and phase mixing in the solar neighbourhood in both action-angle and position-velocity space. A variety of these models were able to produce qualitatively good matches to observational data from the second Gaia data release (DR2), demonstrating some of the inherent difficulty in determining the structure of the Galactic disk from local kinematic data alone.

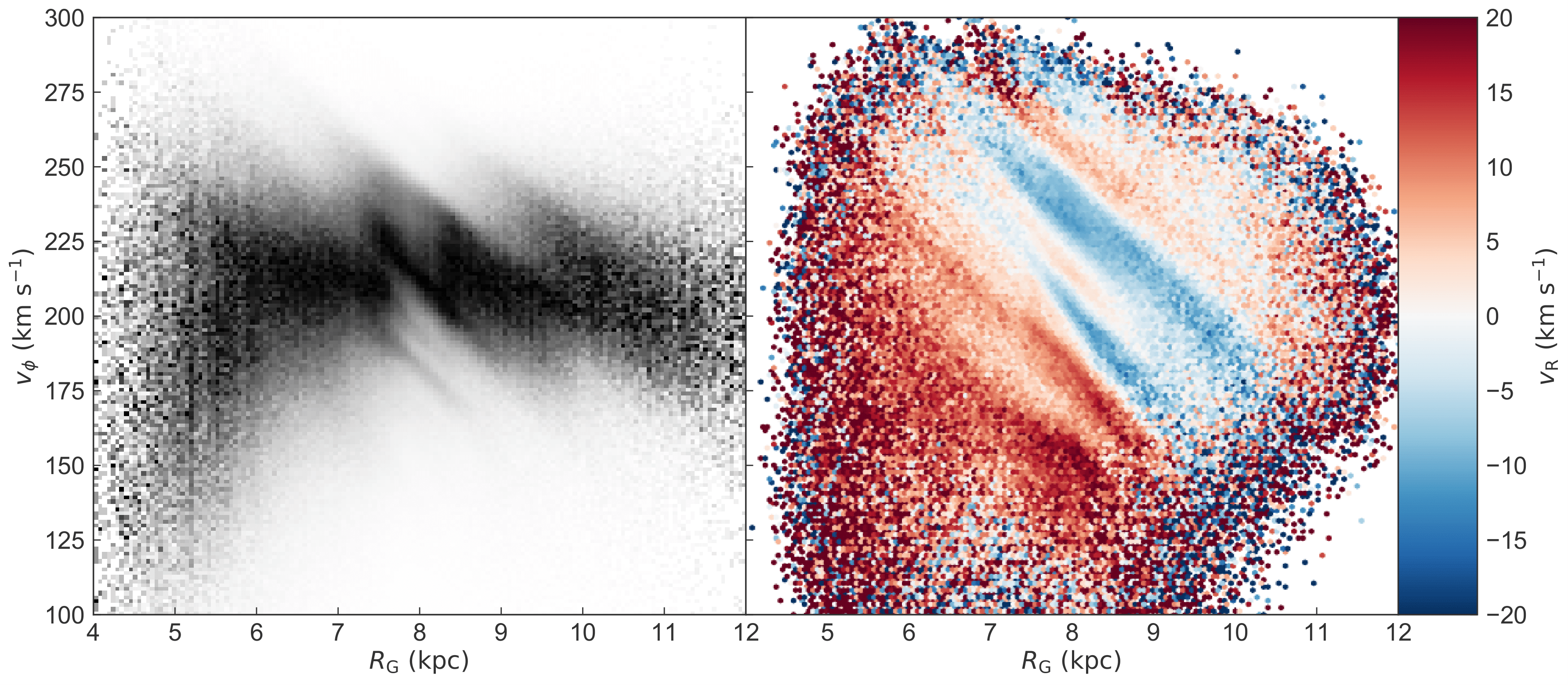Figure 3: The solar neighbourhood in the $R_\mathrm{G}$ – $v_\phi$ plane as seen by Gaia DR2, coloured by both stellar number density and galactocentric radial velocity.

In this project, I was responsible for developing large test particle simulations of the Galactic disk for a variety of Galactic bar and spiral arm models, and to examine how these models produced kinematic signatures in the solar neighbourhood. The simulations, which consisted of over 108 particles each, were performed on the SciNet Niagara cluster.

Galactic Dynamics with Gaia

Supervised by Prof. Jo Bovy

With the second data release (DR2) of the European Space Agency's Gaia mission, a wealth of new possibilities for exploring the kinematic and dynamic properties of the Galaxy have been opened. In this summer project, we investigated how Gaia DR2 might be able to shed light on the third integral of motion in the Milky Way.

It is well known that stellar orbits in the Milky Way are constrained by at least three integrals of motion: energy, axial angular momentum, and a third integral denoted as $I_3$. However, the previous lack of observational data has prevented direct measurement of the third integral in our galaxy. In this project, we applied machine learning techniques to the Gaia DR2 catalogue to recover direct observational evidence of a third integral. We demonstrated that our method is successful at identifying the presence of a third integral in mock data sets, but is limited due to the current incompleteness of the Gaia catalogue. Later data releases of Gaia or more comprehensive astrometric surveys may alleviate these limitations, such that this method of analysis may have potential in the future.

Publications

INSPIRE / ADS / Google Scholar

Quantum gravity background in next-generation gravitational wave detectors
Mathew W. Bub, Yanbei Chen, Yufeng Du, Dongjun Li, Yiwen Zhang, and Kathryn M. Zurek, Phys. Rev. D 108 (2023) 064038.
[arXiv:2305.11224]

Confinement on $\mathbb{R}^3 \times \mathbb{S}^1$ and double-string collapse
Mathew W. Bub, Erich Poppitz, and Samuel S. Y. Wong, JHEP 01 (2021) 044.
[arXiv:2010.04330]

Compact-object Mergers in the Galactic Center: Evolution in Triaxial Clusters
Mathew W. Bub and Cristobal Petrovich, Astrophys. J. 894 (2020) 15.
[arXiv:1910.02079]

Signatures of resonance and phase mixing in the Galactic disc
Jason A. S. Hunt, Mathew W. Bub, Jo Bovy, J. Ted Mackereth, Wilma H. Trick, and Daisuke Kawata, Mon. Not. R. Astron. Soc. 490 (2019) 1026.
[arXiv:1904.10968]